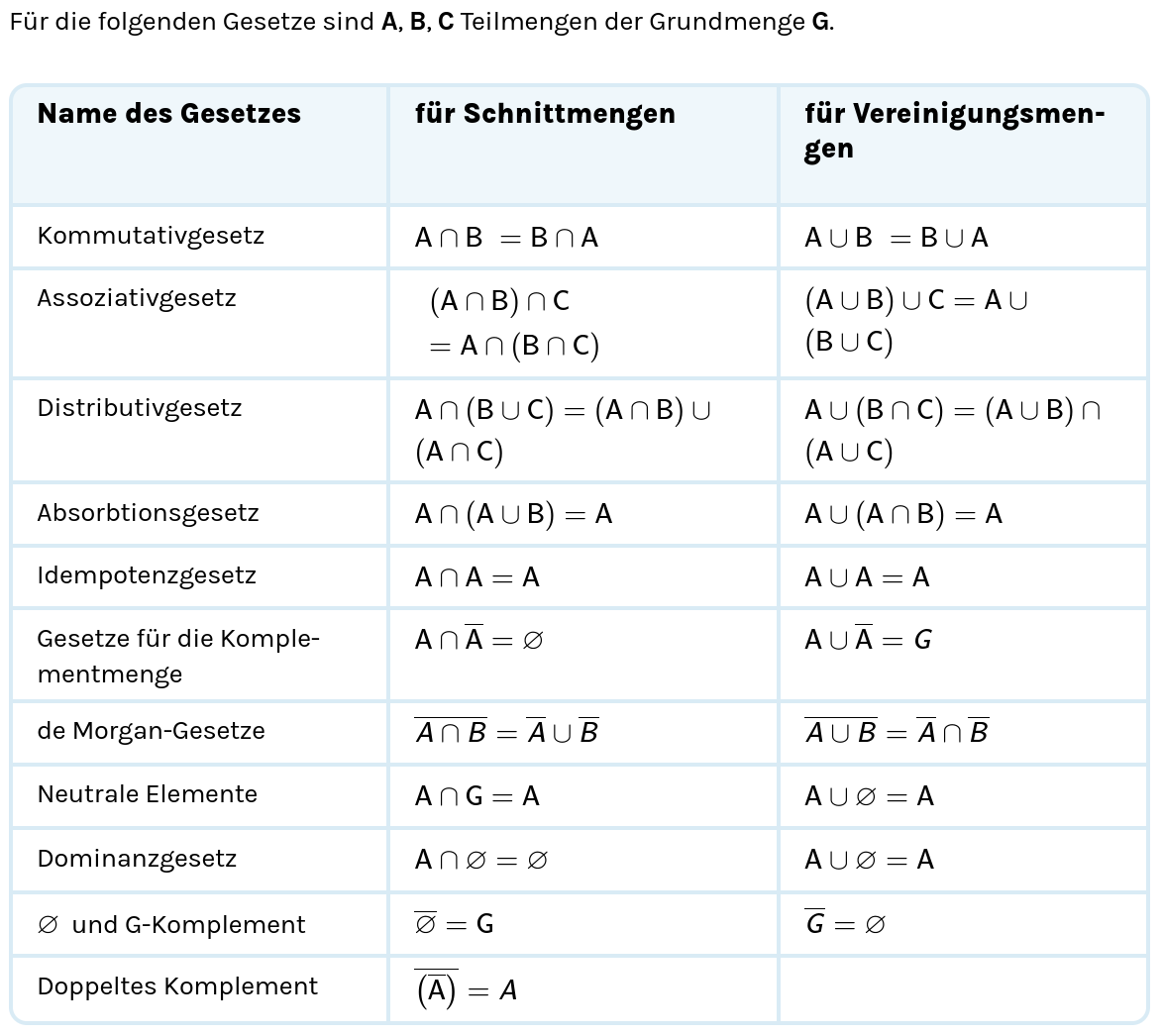
Mengenlehre
Bei relationalen Datenbanken dreht sich alles um Tabellen. Mit Tabellen kann man rechnen: Sie können verbunden werden, vereinigt, geschnitten, und vieles mehr. Das Fundament dafür bildet die Mengenlehre.Eine Menge ist eine Zusammenfassung von unterscheidbaren Objekten, z.B. die Menge $F$ der Farben im Kartenspiel, die Menge $\mathbb{N}$ der natürlichen Zahlen, die Menge $M$ der Musikinstrumente. Man schreibt Mengen häufig in der sogenannten aufzählenden Darstellung, in der diese Objekte einfach aufgezählt werden.
$$ F = \{\unicode{x2660}, \unicode{x2665}, \unicode{x2666}, \unicode{x2663}\} \qquad \text{und} \qquad \mathbb{N} = \{0, 1, 2, 3, ...\} \qquad M = \{\unicode{x1F3BB}, \unicode{x1F3B7}, \unicode{x1F3B8}, ...\} $$Die Objekte, welcher in einer Menge enthalten sind, werden Elemente der Menge genannt. Ein Objekt ist entweder Element ($\in$) oder kein Element ($\notin$) der Menge.
$$ \unicode{x2665} \in F \qquad \text{und} \qquad 2 \in \mathbb{N} \qquad \text{und} \qquad \unicode{x2665} \not\in \mathbb{N} $$Die Elemente sind nicht geordnet, und ebenso kommen Elemente nicht mehrfach vor. Deshalb bezeichnen die folgenden Schreibweisen dieselbe Menge.
$$ \{1, 2\} = \{1, 1, 2\} = \{2, 2, 2, 1\} $$Wie man bei $\mathbb{N}$ sieht, kann eine Menge auch unendlich viele Elemente enthalten. Eine spezielle Menge ist die leere Menge, welche keine Elemente enthält. Man schreibt sie auch als
$$ \{~\} = \emptyset $$Eine Menge $A$ ist Teilmenge einer anderen Menge $B$, geschrieben $A \subseteq B$, wenn jedes Element von $A$ auch in $B$ enthalten ist. Z.B. gilt
$$ \{3, 4, 5\} \subseteq \mathbb{N} \qquad \text{und} \qquad \{3, 4\} \subseteq \{3, 4, 5\} \qquad \text{und} \qquad \{2, 3\} \not\subseteq \{3, 4, 5\} \qquad \text{und} \qquad \mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} $$Eine Eigenschaft wie „ist ein Musikinstrument“ oder „ist eine natürliche Zahl zwischen 1 und 99“ beschreibt gleichzeitig jeweils auch eine Menge, nämlich jene, die alle Musikinstrumente bzw. alle Zahlen zwischen 1 und 99 enthält. Man kann diese Menge dann mit Hilfe dieser Eigenschaft in der folgenden beschreibenden Darstellung angeben.
\begin{tightarray}{rll} M &= \{x ~|~ x~ \text{ist ein Musikinstrument}\}\qquad &\text{„Menge der Musikinstrumente“}\\ &= \{\unicode{x1F3BB}, \unicode{x1F3B7}, \unicode{x1F3B8}, ...\}\\[0.5cm] C &= \{x \in \mathbb{N} ~|~ 1 \le x \le 99\} &\text{„Menge der natürlichen Zahlen zwischen 1 und 99“}\\ &= \{1, 2, 3, ..., 99\} \end{tightarray}Sprich diese zunächst etwas seltsam anmutende Schreibweise so aus:
Oder auch: „$M$ ist die Menge aller $x$, für die gilt: $x$ ist ein Musikinstrument“. Also ist M einfach die Menge aller Musikinstrumente.
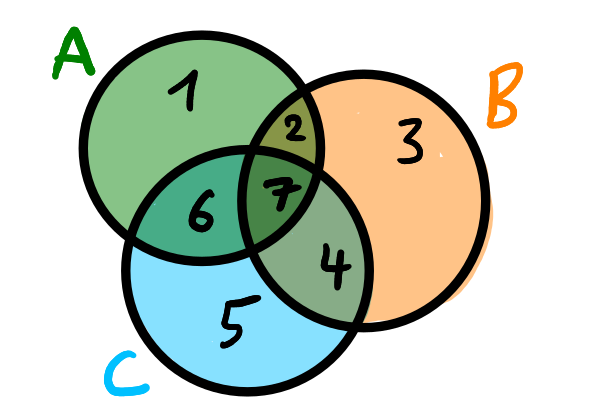
Ein Venn-Diagramm ist eine graphische Darstellung von Mengen. Eine Menge wird als Kreis dargestellt. Die Elemente einer Menge werden dann als Punkte innerhalb des Kreises dargestellt. Die Elemente, die in mehreren Mengen enthalten sind, werden in den Schnittbereichen der Kreise dargestellt.
Mit Mengen kann gerechnet werden. Die wichtigsten Operationen sind Vereinigung, Schnitt und Differenz.
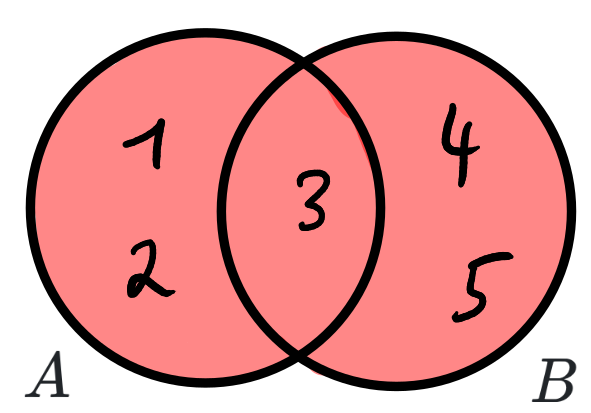
Die Vereinigung zweier Mengen $A$ und $B$ ist die Menge aller Elemente, die in $A$ oder in $B$ enthalten sind (oder in beiden). Man schreibt auch $A \cup B$. Bsp.:
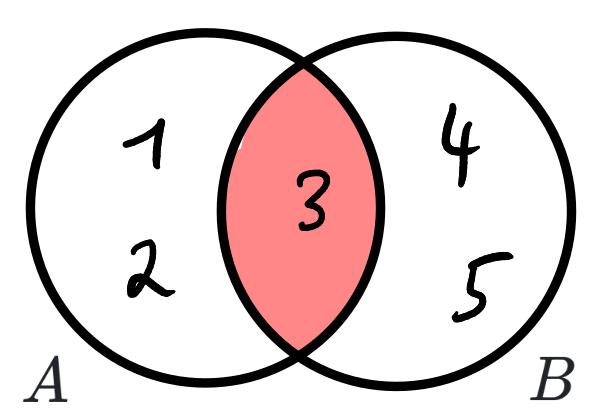
Der Schnitt zweier Mengen $A$ und $B$ ist die Menge aller Elemente, die in $A$ und in $B$ enthalten sind. Man schreibt auch $A \cap B$. Bsp.:
Die Differenz einer Menge $B$ von einer Menge $A$ ist die Menge aller Elemente, die in $A$, aber nicht in $B$ enthalten sind. Man schreibt auch $A \setminus B$. Bsp.:
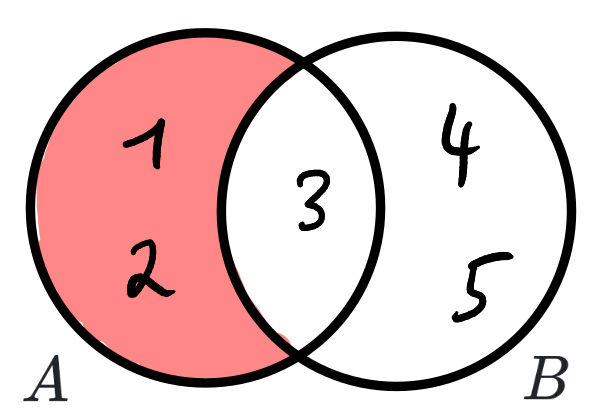
Im Folgenden bezeichnet die Grundmenge $G$ die Menge alle Objekte, die überhaupt betrachtet werden können. Manchmal wird $G$ deshalb auch „Universum“ genannt. Das Komplement $\overline{M}$ einer Menge $M$ beschreibt alle Elemente des Universums (=der Grundmenge), die nicht in $M$ enthalten sind.
